A fourth method for finding reliability, also utilizing a single administration of a single form, is based on the consistency of responses to all items in the test.
Such a formula is developed by Kuder and Richardson (1937). Rather than requiring two-half-scores, this technique is based on an examination of performance on each item.
Of the various formulas developed in the original article, the most widely applicable, commonly known as the Kuder-Richardson formula, is the following:
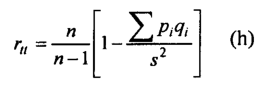
Where n is the number of items on the test, s2 is the variance of the total test scores, and pi is the proportion of persons getting the z-th item correct. The product of p and q is computed for each item, and these products are then summed over all n items to give ∑piqi.
Under the assumption that all items are of equal difficulty, i.e., pi is the same for items, Kuder and Richardson used an alternative tut formula for the above expression in the following form:
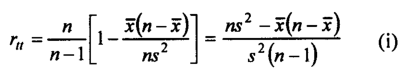
where x, which equals np, is the mean of the total scores. This formula is known as Kuder-Richardson formula 21.
The coefficient computed from formula (i) is a more conservative reliability estimate than that obtained from formula (h). Formula (i), derived from (h) by making pi the same for all items, is simpler from a computational standpoint because the n products piqi do not have to be calculated.
To illustrate the application of formula (i), assume that the mean of a test containing 70 items is 50, and the variance is 100.
Then on applying (h), the estimated reliability of this test is;
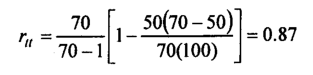
The formula K-R 21 is quick and easy to calculate, and when used appropriately, it can be extremely useful in determining a test’s overall reliability.
Unlike the Split-half method, which splits the test just once, the K-R 21 estimates the reliability of a test that has been split into all possible halves. It automatically corrects for the splits without any need for a Spearman-Brown type adjustment.
To use the K-R 21, the following criteria should be kept in mind:
- The entire test should be aimed at tapping a single domain. If the test is not focused on a single underlying concept, the reliability value will be underestimated
- The test is scored based on each item being either right or wrong.
- All items have about the same degree of difficulty. The formula works best (produces its highest reliability estimate) when the difficulty index is approximately 0.50 for each item.
Nowadays, most researchers use a test of internal reliability known as Cronbach’s alpha (Cronbach, 1951).
It essentially calculates the average of all possible split-half reliability coefficients.
A computed alpha coefficient will vary between ‘1’ (implying perfect internal reliability) and ‘0’ (implying no internal reliability).
A figure of 0.80 is typically employed as a rule of thumb to denote an acceptable level of internal reliability, though many writers work with a slightly lower figure.
The coefficient is defined as;
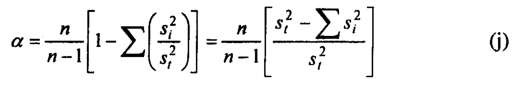
where si2 is the variance of scores on item i, and st2 is the variance of the total test scores. Although the Kuder-Richardson formulas are applicable only when test items are scored “0” (wrong) or ‘1’ (right),
Cronbach’s alpha is a general formula for estimating the reliability of a test consisting of items on which two or more scoring weights are assigned to answers.
Although Cronbach’s alpha has the advantage of identifying which items are or are not contributing to the overall reliability, the disadvantages are that each and every item has to be individually assessed for variability.
What is the primary purpose of the Kuder-Richardson Formula?
The Kuder-Richardson Formula is used for measuring the reliability of a test, specifically focusing on the consistency of responses to all items in the test.
Who developed the Kuder-Richardson Formula and when?
The formula was developed by Kuder and Richardson in 1937.
How is the Kuder-Richardson formula expressed?
The most widely applicable formula, known as the Kuder-Richardson formula, is expressed using the number of items on the test (n), the variance of the total test scores (s2), and the proportion of persons getting the z-th item correct (pi). The product of p and q is computed for each item and summed over all n items.
What is the difference between the Kuder-Richardson formula and Kuder-Richardson formula 21?
The Kuder-Richardson formula 21 is an alternative to the original formula, derived by making pi the same for all items. It is simpler from a computational standpoint as the n products piqi do not have to be calculated.
How does the K-R 21 formula differ from the Split-half method?
Unlike the Split-half method, which splits the test just once, the K-R 21 estimates the reliability of a test that has been split into all possible halves. It corrects for the splits without needing a Spearman-Brown type adjustment.
What criteria should be kept in mind when using the K-R 21?
The criteria include: the test should tap a single domain, the test is scored based on items being either right or wrong, and all items should have about the same degree of difficulty, ideally with a difficulty index of approximately 0.50 for each item.
What is Cronbach’s alpha and how does it relate to the Kuder-Richardson formulas?
Cronbach’s alpha is a test of internal reliability that calculates the average of all possible split-half reliability coefficients. While the Kuder-Richardson formulas are applicable only for test items scored as “0” (wrong) or “1” (right), Cronbach’s alpha can estimate the reliability of a test with items having two or more scoring weights assigned to answers.

