The parallel-forms method, in many instances, is expensive and frequently difficult to construct. Therefore, a less direct method of assessing the effects of different samples of items is the so-called split-half method.
Definition and Meaning Split Half Method
The Split-Half Method is a technique used to assess the reliability of a test by dividing it into two halves and correlating the scores from each half. It evaluates the internal consistency of a test.
To apply the Split-Half Method, a single test is administered, and the entire set of test items is divided into two halves, such as odd-numbered and even-numbered items. The scores from each half are then correlated to compute the reliability coefficient.
What is the significance of the Spearman-Brown prophecy formula in the Split-Half Method?
The Spearman-Brown prophecy formula is used to estimate the reliability of the full test based on the correlation between the two halves. It corrects the reliability coefficient since the correlation from the split-half method gives the reliability of only a half-test.
How does the Split-Half Method differ from other reliability methods?
Unlike the test-retest and parallel-forms reliability methods, where scores are based on the full number of items in the test, the Split-Half Method involves correlating scores based on half the number of items.
What challenges can arise when using the Split-Half Method?
A notable challenge is ensuring that the two halves of the test are comparable, especially in terms of item difficulty. If items are not arranged in an approximate order of difficulty, the two halves might not yield nearly equivalent scores.
How can the reliability of a test be predicted when its length is changed?
The Spearman-Brown formula can be employed to predict the reliability of a test when its length is altered. It can estimate the effect of lengthening or shortening a test on its reliability coefficient.
What is Rulon’s alternative method for finding split-half reliability?
Rulon’s method calculates split-half reliability using only the variance of the differences between each person’s scores on the two half-tests and the variance of total scores. These values are substituted into a specific formula, yielding the reliability of the whole test directly.
How is Split Half Method Administered?
Only one test is administered to compute the reliability coefficient in this technique. The whole set of test items is divided into two halves.
Then a test can be administered, and separate scores assigned to every individual on two arbitrarily selected halves of that test can be obtained.
Example of the split half method
For example, an individual may be given one score on the odd-numbered items and a second score on the even-numbered items.
Then the product moment correlation between the two sets of scores gives the parallel-forms reliability coefficient for a test half as long as the original test.
A notable problem arises in the split-half technique while splitting the test to obtain the most nearly comparable halves.
In most tests, the first and second half would not be comparable owing to differences in nature and difficulty level of items.
A procedure that is adequate for most purposes is to find the scores on odd and even-numbered test items. If the items were originally arranged in approximate order of difficulty, such a division yields nearly equivalent halfscores.
Once the two-half scores have been obtained for each individual, they may be correlated by the usual method. It should be noted.
However, that correlation gives the reliability of only a half-test.
For example, if the entire test consists of 100 items, the correlation is computed between sets of scores, each of which is based on only 50 items.
In both test-retest and parallel-forms reliability, on the other hand, each score is based on the full number of items in the test.
Assuming that the two halves are equivalent, the reliability of the full test ( rtt ) can be estimated by means of the Spearman-Brown prophecy formula, as given below.
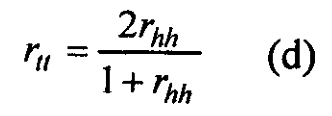
Where rhh is the correlation between the half test. As an example, if the correlation of the total scores on the odd-numbered items with the total scores of the even-numbered items is 0.80, the estimated reliability of the whole test is

The Spearman-Brown prophecy formula stated in (d) above is a particular case of a more general formula of the following type:
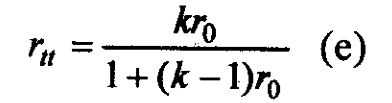
in which k is the factor by which the test is to be lengthened or shortened concerning the original test whose reliability coefficient is ro.
The formula (e) is of particular significance. It estimates the effect of lengthening or shortening a test on its reliability coefficient.
Suppose we have an n1 item test, and we know its reliability, which is r0.
By the use of this formula, we can predict what its reliability would be if n2 additional similar items were added to the test. Here k = ( n1 + n2 ) / n1 . Substituting k in (e), the reliability coefficient of the new test can be calculated.
Similarly, if we have an m1 item test of known reliability and we wish to reduce it to a test of m2 item (m2 < m1), the Spearman-Brown formula may be employed with k = ( m1 – m2 ) to estimate the reliability of the shortened test.
In addition, the formula is useful when we want to determine how many items will be needed to achieve a given level of reliability.
For instance, if rtt were set at 0.9, we can determine how many items would be needed, inter-correlating 0.5 to achieve this desired level of reliability.
This can be obtained from the following formula.
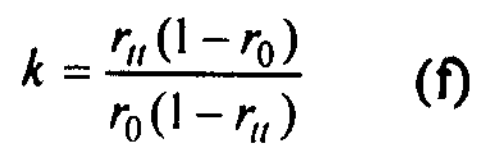
The formula can easily be obtained from a sample rearrangement of (e). Setting rtt=0.90, and ro=O.5O, we find;
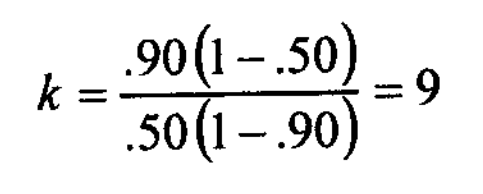
This demonstrates the main justification for including a number of items in a test (or scale) that the reliability can thereby be increased to a satisfactory level.
The formula further shows that the number of items needed to reach a given level of reliability depends on the homogeneity of the items that are on the inter-correlations between them.
Examples of Split Half Method
Example #1
Suppose we have a 20-item test with a reliability coefficient.
0.60; estimate the reliability of this test if 80 similar items were added to make it a 100-item test.
Solution: In this instance k = ( n1 + n2 ) / n1 = (20 + 80 ) / 20 = 5 and r0 = 0,60.
Hence using (e);
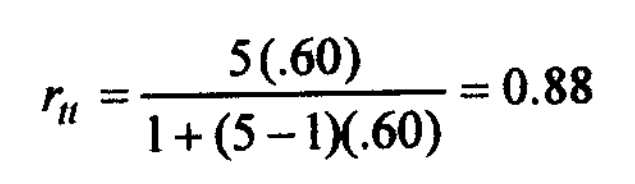
Example #2
Suppose we have a 110-item test, the length of which is reduced to 55 items. The reliability coefficient of the original test is 0.80. What would be the reliability of the shortened test?
Solution: Here k = ( m1 – m2 ) / m1 = ( 110 – 55 ) 110 = 0.50 and r0 = 0.80.
Hence;
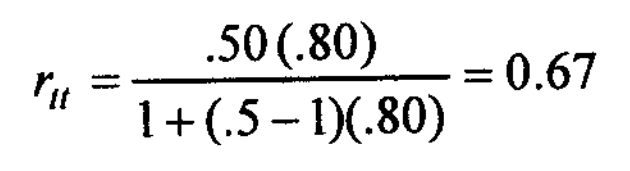
An alternative method for finding split-half reliability was developed by Rulon (1939).
It requires only the variance of the differences between each person’s scores and the two half-tests ( s2e ) and the variance of total scores ( s2t ); these two values are substituted in the following formula, which yields the reliability of the whole test directly:
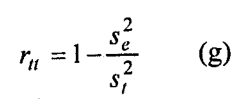
Thus for a test with a standard deviation of 6 and a standard error of measurement of 3, Rulon’s method gives a reliability coefficient of;
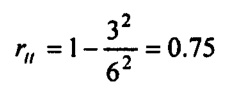
Example #3
A sample of ten students, all of the same age, was selected and given a Math test to assess strengths and weaknesses in a number of math and math-related areas.
Use the split-half method with a Spearman-Brown correction for the desired assessment. The scaled scores for the odd and even items are shown in the accompanying table.
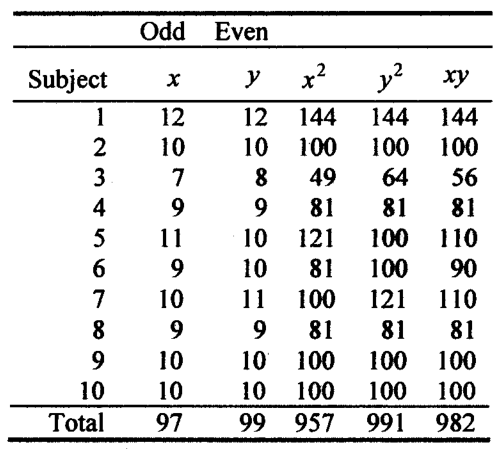
The computed correlation coefficient is;
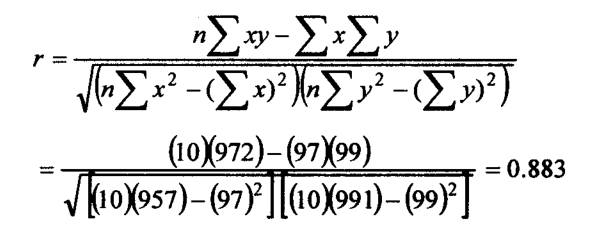
With 8 df, the r is significant at a 1% level (for r to be significant, a table value of 0.765 is required). Since r is significant, we apply the Spearman-Brown formula as follows:
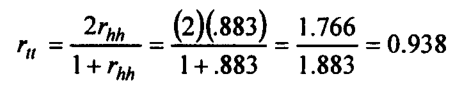
The reliability is thus established at 0.938, which is certainly a lofty value and indicates a high degree of reliability.

