Systematic sampling is a more simplified and versatile probability sampling method where researchers select members of the population at a regular interval.
While discussing simple random and stratified sampling designs, we have noted that both designs require somewhat laborious work in the sample selection process.
For both designs, an adequate sampling frame must be available, and the sampling units thereof must be numbered or otherwise identified so that a randomization device, such as a random number table, can select the specific units.
In such instances, a more simplified and versatile form of probability sampling design, known as systematic sampling, can be employed.
If employed with care, the systematic sampling design simplifies much of the work in simple random or stratified sampling.
In addition to its being operationally more convenient than simple random sampling, it ensures for each unit an equal probability of inclusion in the sample.
In selecting a sample of n units from a population of N units when N=nk using a systematic sampling approach, we follow the following steps:
- List the units giving a serial number from 1 to N.
- Determine the sampling interval k dividing TV by k = N/n.
- Select a random number between 1 and k. Say this is r. Your first selected unit is r.
- Add k to Your second selected unit bears the serial number r+k.
- Next, add 2k to r so that your third selected unit bears the serial number r+2k.
- Continue the process, and finally, the n-th unit will bear the serial number r+(n-V)k.
Example #1
Suppose a population consists of 15 units, numbered serially from 01 to 15, and that a random sample of 3 units is desired. This gives rise to a sampling interval of 15/3=5. We now select one of the first five units randomly, 01 to 05, and then every 5th unit in the sequence.
For example, if the first unit is 03, then the sample will consist of units 03, 08, and 13; if the first unit is 01, the sample will consist of units 01, 06, and 11.
The resulting sample is called every k-th or 1-in-k systematic sample.
Note that selecting the first unit from among the first k units determines the whole sample.
The sampler thus can set k to be any number he/she wishes, depending upon the proportion of the sampling fraction needed in the whole sample.
The procedure is termed systematic linear sampling so long as N = nk If N is not an exact multiple of k i.e. N ≠ nk, a systematic sample will contain either n or n-1 units depending on the serial number of the first selected unit. Such a method will be called a circular systematic sampling method.
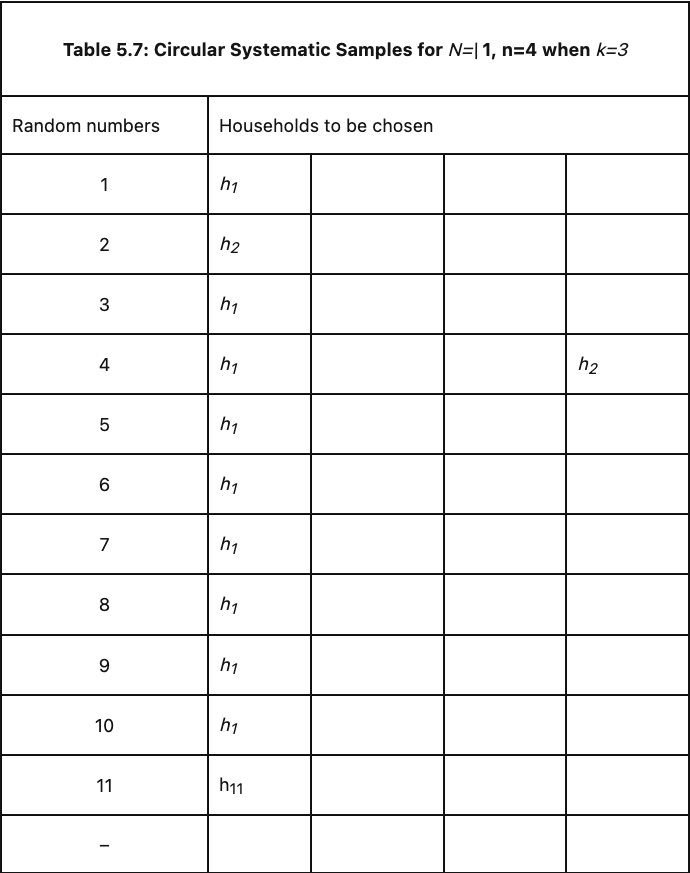
Example#2
Suppose a village consists of 11 households labeled h1; h2, …,h11, from which a sample of 4 households is to be chosen. The sampling interval k is 11/4=2.75, which we approximate to the next higher integer 3.
The procedure consists in selecting a household by a random number between 1 and 11 inclusive and taking every 3rd household thereafter going around the circle until the desired 4 households have been chosen.
In this method, the random number “r” can be chosen entirely randomly from among the 11 households. The selection process is continued beyond 11 by renumbering the households numbered 1, 2, 3, etc. as 12, 13, 14, etc.
The table below illustrates the selection procedure following the circular systematic sampling method.