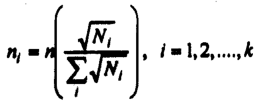A restricted sampling design, which can be more efficient than simple random sampling, is stratified random sampling.
Stratified Random Sampling: Meanings, Procedure,Types, Examples
What is Stratified Random Sampling?
The procedure requires that we have prior knowledge of the population. The stratification process involves dividing the population into several non-overlapping groups or classes called strata.
Within each such stratum, the items are more alike (homogeneous) than are the items in the population as a whole concerning the characteristics to be studied.
That is, you create a set of homogeneous samples based on the variables you are interested in studying.
From each stratum, a sub-sample is taken by the simple random sampling procedure, and the overall sample is obtained by combining the sub-samples for all strata.
University students, for example, can be divided or stratified by their faculty level (Science, Arts, Commerce, etc.), religion (Muslim, Hindu, Buddhist, etc.), gender (Male, Female), and so forth.
After this stratification, simple random samples of the desired size can be taken within each stratum.
The sampling results can then be weighted and combined into appropriate population estimates.
Specifically, the stratification process possesses the following salient features:
- The entire population is divided into several distinct subpopulations, called strata;
- Within each stratum, a separate and independent sample is selected;
- For each stratum, stratum mean, proportion, variance, and other statistics are computed;
- These estimates are then properly weighted to form a combined estimate for the entire population.
Example of Stratified Random Sampling
Suppose a population comprises 700 Muslims, 200 Hindus, and 100 Christians.
If a simple random sample of 100 persons (10% of the total) is desired, we would probably not get exactly 70 Muslims, 20 Hindus, and 10 Christians: the proportion of Christians, in particular, might be too small.
A stratified sample of 70 Muslims, 20 Hindus, and 10 Christians would ensure a better representation of the groups.
Strata are generally formed based on the primary variable under investigation.
If the researcher had wished to ensure that religions were adequately represented in the sample, he could have stratified the students by their religion. Religion is then called a stratification factor or stratification variable.
It is important to note that there will be no gain in precision from stratification by a factor unrelated to the subject of the study, for the characteristics of the different strata would not differ from each other, and nothing would be gained by excluding from the sampling error the between-strata variation.
Thus, ideally, one wishes to stratify a sample by the factors believed to be most closely related to the subject of the study.
Suppose the researcher, for instance, studying the living and working conditions of the people, had wished to ensure that different types of areas (e.g., City Corporation, Municipal area, urban, semi-urban, rural, etc.) were adequately represented in the sample.
In that case, he could have stratified the population by area type.
Here, area type is the stratification variable, which is clearly related to the study variables (viz., living and working conditions).
In studying the television viewing habit among university students, academic performance scores (high, medium, low) or the place of residence (urban, rural) may serve as stratification variables since each of these variables is believed to be related to the television viewing habit of the students.
Allocating sample size to strata
Once we specify the total number n of observations to be included in the sample, the next important task is to decide on the number of observations to be taken from each individual stratum under the constraint that a total of n observations or elements are to be taken over all strata.
This is what is known as the problem of allocation.
Assuming that the overall sample size n is fixed, it is not immediately obvious what the values of nx,n2,…,nk should be such that nx+n2+… + nk =n.
It is, therefore an important consideration to delineate some rules or principles for allocating sample sizes to different strata.
Types of Stratified Random Sampling Procedure
There are usually four sample size allocation methods to different strata in a stratified sampling procedure. These are,
- Arbitrary Allocation
- Equal Allocation
- Proportional Allocation
- Kish Allocation
- Square Root Allocation
Arbitrary Allocation
In this allocation, the choice of the sample size for different strata depends entirely on the convenience of the sampler.
This is thus a purposive allocation. The only restriction is that sum of the sample sizes in different strata will add to n, the total sample size. That is,
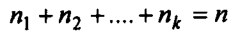
Equal Allocation
The same number of elements is drawn from each stratum in this allocation. In other words, for stratum i, the sample size is given by
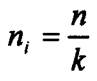
where n, is the size of the sample to be drawn from the z-th stratum, n is the overall sample size, and k is the number of strata in the population.
Thus, for example, if a population consists of k=4 strata and a sample of n=500 is to be allocated to these strata, then the principle of equal allocation asserts that ni = 500/4 = 125. This implies that 125 units will be drawn from each of the four strata.
The equal allocation approach is of considerable practical interest for reasons of administrative convenience or ease in fieldwork.
This allocation will be the allocation of choice if the primary objective of the sample survey is to test the hypotheses about differences among the strata with respect to levels of variables of interest, under the assumption that within-stratum variations are equal.
Proportional Allocation
Sampling within each stratum may be made proportionately or disproportionately. A proportionate stratified sample is achieved if every stratum’s sampling fraction (n/N) is the same (i.e., uniform).
Under this design, items in the sample are allocated among the strata in proportion to the relative number of items in each stratum in the population.
Stratified sampling with a uniform sampling fraction tends to have greater precision than simple random sampling, and it is also generally convenient for practical reasons.
But it is, of course, vital that the selection within strata is made randomly.
In this procedure, the items in the sample are allocated among the strata in proportion to the relative number of items in each stratum in the population.
That is to say, the larger the stratum size, the larger the size of the sample to be chosen from that stratum. This is perhaps the most widely used method of allocation.
If nt represents the sample size and TV, the population size in the z-th stratum, then the sampling fraction ni/Ni is specified to be the same for each stratum. This also implies that the overall sampling fraction n/N is the fraction taken from each stratum. In other words, the number of elements ni took from each stratum is given by;
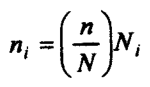
This equation implies that proportionally allocated stratified sampling gives each sampling unit the same probability of selection in the entire population.
Thus if N=300 and n=30, then 10% of the observations from each stratum are to be included in the sample.
Kish Allocation
The proportional allocation assigns a small proportion of the sample too small strata.
This may be a problem when the main strata are administrative regions of a country for which separate estimates are required and when the divisions differ greatly in size.
When this is the case, the equal allocation will result in substantial variation in the sampling fractions between strata.
This will lead to a larger sampling fraction for the smallest stratum than the fraction for the most populous strata.
A compromise between proportional and equal allocation is the allocation proposed by Kish, known as Kish allocation.
The formula for Kish allocation appears below:

Square Root Allocation
One more allocation is frequently used, known as square root allocation.
This is formulated as follows: