The reliability of a test may be expressed in terms of the standard error of measurement (se), also called the standard error of a score. This score is particularly well suited to the interpretation of individual scores.
It is, therefore, more useful than the reliability coefficient for many testing purposes. The standard error of measurement can be easily computed from the reliability coefficient of the test by a simple rearrangement of the Rulon formula (g):
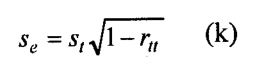
In which it is the standard deviation of the test scores and rtt the reliability coefficient, both computed on the same group.
The standard error of measurement is a useful statistic because it enables an experimenter to estimate limits within which the true scores of a certain percentage of individuals (subjects) having a given observed score can be expected to fall, assuming that errors of measurement are normally distributed.
According to the normal law of probability, about 68% (more precisely, 68.27%) of a group of individuals will have true scores falling within ±1 standard error of the measurement of the observed score.
Likewise, about 95% of a group of individuals having the same observed scores will have true scores falling within ±2 standard error of the measurement of the observed score.
And virtually all (99.72%) will have true scores falling within +3 the standard error of the measurement of that observed score.
As an example, assume that the standard deviation of the observed scores on a test is 10 and the reliability coefficient is 0.90; then;
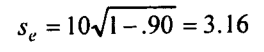
So if a person’s observed score is 50, it can be concluded with 68.27% confidence that this person’s true score lies in the interval 50 ±1(3.16), i.e., between 46.84 and 53,16. If we want to be more certain of our prediction, we can choose higher odds than the above.
Thus, we are virtually certain (99.72%) that this individual will have his true score in the range of 40.52 and 59.48, resulting from the interval of 50±3(3.I6).
As formula (k) shows, the standard error of measurement increases as reliability decreases. When rn=1.0, there is no error in estimating an individual’s true score from the observed score.
When rn=.00, the error of measurement is a maximum and equal to the standard deviation of the observed score.
Of course, a test with a reliability coefficient close to 0.00 is useless because the correctness of any decisions made on the basis of the scores will be no better than chance.
How do we judge the usefulness of a test in terms of the reliability coefficient?
The answer to this question depends on what one plans to do with the test score.
If a test is used to determine whether the mean scores of two groups of people are significantly different, then a reliability coefficient as low as 0.65 may be satisfactory. If the test is used to compare one individual with another, a coefficient of at least 0.85 is needed.
Conclusion
The standard error is the standard deviation of the sample distribution. It measures the amount of accuracy by which a given sample represents its population.
How is the standard error of the mean (SEM) defined?
The standard error of the mean, abbreviated as SEM, represents the standard deviation of the measure of the sample mean of the population. It defines an estimate of standard deviation computed from the sample.
How is the standard error different from standard deviation?
While standard deviation measures the variability or dispersion from the mean, the standard error indicates how precisely a sample represents its population. The standard error is calculated by dividing the standard deviation by the square root of the sample size.
What is the significance of the standard error of estimate (SEE)?
The standard error of the estimate (SEE) estimates the accuracy of predictions. It represents the deviation of estimates from intended values and is also known as the sum of squares error.
How can the standard error be calculated?
The standard error is calculated by determining the standard deviation (σ) and then dividing it by the square root of the number of measurements (n).
Why is the standard error important in statistics?
Standard errors provide simple measures of uncertainty in a value. They help in understanding the precision of a sample mean about the population mean. A smaller standard error indicates that the sample mean reflects the actual population mean more accurately.
Is the standard error the same as the standard error of the mean (SEM)?
The standard error (SE) can be more precisely defined as the mean (SEM) standard error. It is a property of the estimate of the mean and shows the precision of the sample mean compared to the population mean.

