Recall that statistics often aims to make inferences about unknown population parameters based on information contained in sample data. These inferences are phrased in two ways;
- as estimates of the respective parameters or
- as tests of hypotheses about their values.
In many ways, the formal procedure for hypothesis testing is similar to the scientific method. The scientist observes nature, formulates a theory, and then tests this theory against observations.
Learn Hypothesis Testing.
In our hypothesis-testing context, the researcher sets up a hypothesis concerning one or more population parameters-that they are equal to some specified values.
He then samples the population and compares his observations with the hypothesis. If the observations disagree with the hypothesis, the researcher rejects it.
If not, the researcher concludes that the hypothesis is true or that the sample failed to detect the differences between the true value and hypothesized value of the population parameters.
Examine the following cases:
- A biochemist may wish to determine the sensitivity of a new test for the diagnosis of cancer;
- A production manager asserts that the average number of defective assemblies (not meeting quality standards) produced each Day is 25;
- An Internet server may need to verify if computer users in the country spend, on average more than 20 hours on browsing;
- A medical researcher may hypothesize that a new drug is more effective than another in combating a disease;
- An electrical engineer may suspect that electricity failure in urban areas is more frequent in rural areas than in urban areas.
Statistical hypothesis testing addresses the above issues with the obtained data. We may now put forward the following definition of a statistical hypothesis.
Hypothesis Meaning
A statistical hypothesis is a statement or assumption regarding one or more population parameters. Our aim in hypothesis testing is to verify whether the hypothesis is true or not based on sample data.
The conventional approach to hypothesis testing is not to construct a single hypothesis but to formulate two different and opposite hypotheses.
These hypotheses must be constructed so that if one hypothesis is rejected, the other is accepted and vice versa. These two hypotheses in a statistical test are normally referred to as null and alternative hypotheses.
The null hypothesis, denoted by Ho, is the hypothesis to be tested. The alternative hypothesis, denoted by H1 is the hypothesis that, in some sense, contradicts the null hypothesis.
Example #1
A current area of research interest is the familial aggregation of cardiovascular risk factors in general and lipid levels in particular. Suppose it is known that the average cholesterol level in children is 175 mg/dl. A group of men who have died from heart disease within the past year is identified, and the cholesterol levels of their offspring are measured.
We want to verify if
- The average cholesterol level of these children is 175 mg/dl.
- The average cholesterol level of these children is greater than 175 mg/dl.
This type of question is formulated in a hypothesis-testing framework by specifying the null and alternative hypotheses. In the example above, the null hypothesis is that the average cholesterol level of these children is 175 mg/dl.
This is the hypothesis we want to test. The alternative hypothesis is that the average cholesterol level of these children is greater than 175 mg/dl. The underlying hypotheses can be formulated as follows;
| Null Hypothesis | H0 : μ = 175 |
| Alternative Hypothesis | H1 : μ > 175 |
We also assume that the underlying distribution is normal under either hypothesis. These hypotheses can be written in more general terms as follows:
| Null Hypothesis | H0 : μ = μ0 |
| Alternative Hypothesis | H1 : μ > μ1 |
We may encounter two types of error in accepting or rejecting a null hypothesis. We may wrongly reject a true null hypothesis. This leads to an error, which we call a type I error.
The second kind of error, called type II error, occurs when we accept a null hypothesis when it is false, that is, when an alternative is true.
When no error is committed, we arrive at a correct decision. The correct decision may be achieved by accepting a true null hypothesis or rejecting a false null hypothesis. Four possible outcomes with associated types of error that we commit in our decision are shown in the accompanying table:
| Decision | Ho is true | Hi is true |
| Reject Ho | Type I error P(Type I error) = α | Correct decision P(Correct decision) = 1 – ß |
| Accept Ho | Correct decision P(Correct decision) = 1-α | Type II error P(Type II error) = ß |
The probability of committing a type-I error is usually denoted by a and is commonly referred to as the level of significance of a test:
α = P (type I error) = P(rejecting H0 when H0 is true )
The probability of committing a type II error is usually denoted by ß:
ß = P (type II error) = P (accepting H0 when is H1 true )
The complement of ß, i.e. 1- ß is commonly known as the power of a test.
1- ß = 1 – P = P (rejecting H0 when H1 is true )
What are the type I and type II errors for the data in Example#1?
The type I error will be committed if we decide that the offspring of men who have died from heart disease have average cholesterol greater than 170 mg/dl when their average cholesterol level is 175 mg/dl.
The type II error will be committed if we decide that the offspring have normal cholesterol levels when, in fact, their cholesterol levels are above average.
Significance Level
The significance level is the critical probability in choosing between the null and the alternative hypotheses. The probability level is too low to warrant the support of the null hypothesis.
The significance level is customarily expressed as a percentage, such as 5% or 1%. A significance level of, say 5% is the probability of rejecting the null hypothesis if it is true.
When the hypothesis in question is accepted at the 5% level, the statistician is running the risk that, in the long run, he will be making the wrong decision about 5% of the time.
Test Statistic
The test statistic (like an estimator) is a function of the sample observations upon which the statistical decision will be based. The rejection region (RR) specifies the values of the test statistic for which the null hypothesis is rejected in favor of the alternative hypothesis.
If, for a particular sample, the computed value of the test statistic falls in RR, we reject the null hypothesis Ho and accept the alternative hypothesis H1.
If the value of the test statistic does not fall into the rejection (critical) region, we accept Ho. The region other than the rejection region is the acceptance region.
Making Decision
A statistical decision is either to reject or accept the null hypothesis. The decision will depend on whether the computed value of the test statistic falls in the region of rejection or the region of acceptance.
Suppose the hypothesis is being tested at a 5% significance level, and the observed results have probabilities less than 5%. In that case, we regard the difference between the sample statistics and the unknown parameter as significant.
In other words, we think the sample result is so rare that it cannot be explained by chance variation alone. We then reject the null hypothesis and state that the sample observations are inconsistent with the null hypothesis.

On the other hand, if at a 5% level of significance, the observed set of values has a probability of more than 5%, we give a reason that the difference between the sample result and the unknown parameter value can be explained by chance variation and therefore is not statistically significant.
Consequently, we decide not to reject the null hypothesis and state that the sample observations are not inconsistent with the null hypothesis.
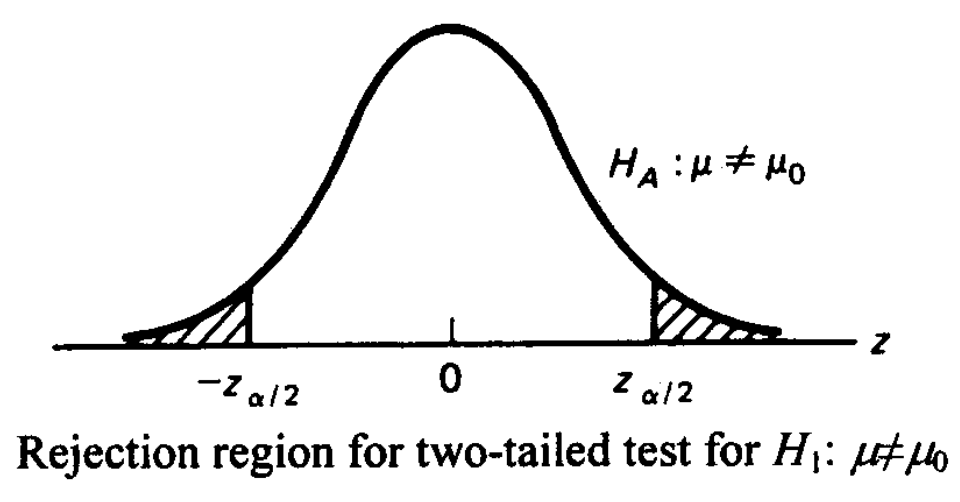
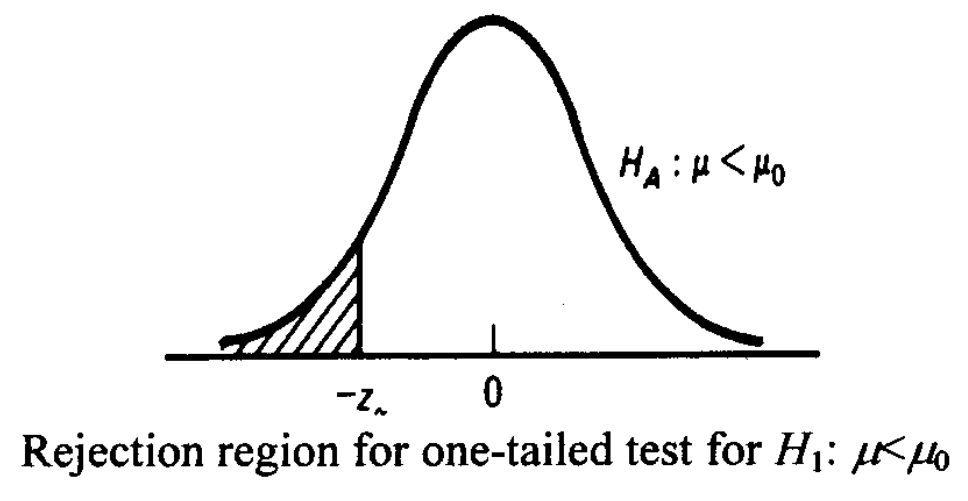
One-tailed and Two-tailed Test
A one-tailed test is a test in which the values of the parameter being studied (in our previous example, the mean cholesterol level) under the alternative hypothesis are allowed to be either greater than or less than the values of the parameter under the null hypothesis, but not both.
That is, we formulate null and alternative hypotheses for a one-tailed test as follows:
| Null Hypothesis | H0 : μ = μ0 |
| Alternative Hypothesis | H1 : μ < μ0 or μ > μ0 |
A two-tailed test is a test in which the values of the parameter being studied under the alternative hypothesis are allowed to be greater than or less than the values of the parameter under the null hypothesis.
We formulate the hypotheses under the two-tailed test as follows:
| Null Hypothesis | H0 : μ = μ0 |
| Alternative Hypothesis | H1 : μ ≠ μ1 |
It is very important to realize whether we are interested in a one-tailed or two-tailed test in a particular application.
p-Value and Its Interpretation
There are two approaches to testing a statistical hypothesis: critical value method and 72-value method.
The general approach where we compute a test statistic and determine the outcome of a test by comparing the test statistic to a critical value determined by the type I error is called the critical-value method of hypothesis testing.
The p-value for any hypothesis test is the alpha (a) level at which we would be indifferent between accepting and rejecting the null hypothesis given the sample data at hand.
That is, the value is the level at which the given value of the test statistic (such as t, F, chi-square) would be on the borderline between the acceptance and rejection regions.
The p-value can also be thought of as the probability of obtaining a test statistic as extreme as or more extreme than the actual test statistic obtained, given the null hypothesis is true.
Statistical data analysis programs commonly compute the p-values during the execution of the hypothesis test. The decision rules, which most researchers follow in stating their results, are as follows:
- If the p-value is less than .01, the results are highly significant.
- If the p-value is between .01 and .05, the results are considered statistically significant.
- If the p-value is between .05 and .10, the results only tend toward statistical significance.
- If the p-value is greater than .10, the results are considered insignificant.
Steps in a Statistical Test
Any statistical test of hypotheses works similarly and is composed of the same essential elements. The general procedure for a statistical test is as follows:
- Set up the null hypothesis (Ho) and its alternative (Ht). It is a one-tailed test if the alternative hypothesis states the direction of the difference. If no direction of difference is given, it is a two-tailed test.
- Choose the desired level of significance. While α=0.05 and α=0.01 are the most common, many others are also used.
- Compute the sample data’s appropriate test statistic (normal, t).
- Find the critical value(s) using normal integral tables corresponding to the critical region established.
- With the critical values determined in step 4, compare the test statistic computed in step 3.
- Make the decision: reject the null hypothesis if the computed test statistic falls in the critical region and accept the alternative (or withhold the decision)
Some Commonly Used Tests of Significance
This section provides an overview of some statistical tests representative of the vast array available to researchers.
This section recognizes two general classes of significance tests: parametric and non-parametric.
Statistical procedures that require the specification of the probability distribution of the population are referred to as parametric tests.
In contrast, non-parametric procedures are distribution-free approaches requiring no specification of the underlying population distribution.
Parametric tests are more powerful because their data are derived from interval and ratio measurements.
Nonparametric tests are used to test hypotheses with nominal and ordinal data. Our aim in this text is to discuss the parametric tests in common use primarily.
Assumptions for parametric tests include the following:
- The observations must be independent.
- The observations are drawn from normal populations.
- The populations should have equal variances.
- The measurement levels should be at least interval.
In attempting to choose a particular significance test, one should consider at least three points:
- Does the test involve one sample, two samples, or k-samples?
- Are the individual cases in the samples independent or dependent?
- Which levels of measurement do the data refer to nominal, ordinal, interval, or ratio?
Considering the above queries, we will discuss some common tests of significance. These include, among others.
- The normal tests
- The t-tests
- The chi-square test
- The F-test
What is the primary aim of hypothesis testing in statistics?
The primary aim of hypothesis testing in statistics is to make inferences about unknown population parameters based on information contained in sample data. These inferences can be phrased as estimates of the parameters or as tests of hypotheses about their values.
What are the two main hypotheses used in a statistical test?
The two main hypotheses used in a statistical test are the null hypothesis (Ho) and the alternative hypothesis (H1). The null hypothesis is the hypothesis to be tested, while the alternative hypothesis contradicts the null hypothesis in some sense.
How is a one-tailed test different from a two-tailed test?
A one-tailed test is a test in which the values of the parameter being studied under the alternative hypothesis are allowed to be either greater than or less than the values of the parameter under the null hypothesis, but not both. A two-tailed test allows the values of the parameter under the alternative hypothesis to be greater than and less than the values under the null hypothesis.
What is the significance level in hypothesis testing?
The significance level is the critical probability in choosing between the null and the alternative hypotheses. It represents the probability level that is too low to warrant the support of the null hypothesis. Common significance levels include 5% or 1%.
What are type I and type II errors in hypothesis testing?
A type I error occurs when a true null hypothesis is wrongly rejected. A type II error occurs when a false null hypothesis is wrongly accepted. The probability of committing a type I error is denoted by α, and the probability of committing a type II error is denoted by ß.
How is the p-value used in hypothesis testing?
The p-value is the probability of obtaining a test statistic as extreme as or more extreme than the actual test statistic obtained, given the null hypothesis is true. It helps in determining the significance of the results. If the p-value is less than the chosen significance level, the null hypothesis is rejected.
What are some common tests of significance in statistics?
Some common tests of significance include the normal tests, t-tests, chi-square test, and F-test. The choice of test depends on factors like the number of samples, independence of cases, and the level of measurement of the data.

