Experimental research design is an elegant way to determine how well a particular program achieves its goals. Many experimental designs vary widely to control the contamination of the relationship between independent and dependent variables.
Understand Experimental Research Design.
What is an Experimental Study?
An experimental study is one in which the researcher manipulates the situation and measures the outcome of his manipulation. This contrasts with a correlational study, which has very little control over the research environment.
The experimental study exercises considerable control over the environment. This control over the research process allows the experimenter to attempt to establish causation rather than mere correlation. Thus the establishment of causation is the usual goal of the experiment.
The classical experimental study has three characteristics:
- Manipulation;
- Control and
- Randomization.
Individuals in an experimental study are randomly selected and allocated to at least two groups. One group is subject to intervention (or manipulation or test stimulus), while the other group(s) is not.
In a true experimental study, the experimenter can measure the values of the dependent variable both before administering the stimulus (the pretest) and after administering it (the posttest).
The difference between these scores gives a rough indication of the effect of the causal variable. The group to which the test stimulus or manipulation is administered is called the experimental group. The group that does not receive the test stimulus is called the control group.
We further elaborate on the terms control and randomization.
By control, we mean all factors except the independent variable must be held constant and not confounded with another variable (extraneous variable), that is not part of the study.
By randomization, we mean that the researcher takes care to assign subjects to the control and experimental groups randomly. Each subject is given an equal chance of being assigned to either group.
The goal of all selection procedures for experimental and control groups is to make the groups as similar as possible in terms of the dependent variable and thus, necessarily in terms of all factors affecting it.
Therefore, pretest scores for the experimental and control groups will ideally be identical or similar before the introduction of the test stimulus. Randomization does not necessarily ensure that pretest scores for the two groups will be identical.
However, it should ensure that whatever differences do remain, are random, by which we mean differences are chance outcomes.
The basic logic of experimentation is quite simple. The experimenter begins with a causal hypothesis, which states that one variable (the independent variable) causes changes in a second variable (the effect or dependent variable).
The next step is to;
- measure the dependent variable (pretest);
- introduce the independent variable to the situation or change its level if it is already present, and
- measure the dependent variable (posttest) to see whether there has been any resultant change in its value.
One important question that arises in an experimental study is: how does one separate the portion of a total change in pretest and posttest scores, which is caused by extraneous factors from the portion that is caused by the test stimuli?
This cannot be done with a. single group of subjects but can be accomplished with two groups if certain assumptions can be made.
The assumptions are
- The subjects in the two groups (experimental and control) are identical in their characteristics;
- The pretest plus any extraneous factors that affect one group will also affect the second group to the same degree.
The first assumption implies that the average pretest scores should be identical. In contrast, assumption 2 ascertains that the difference between pretest and posttest scores that is caused by extraneous factors is the same in each group.
If these assumptions hold, one pretests both groups but administers the causal stimulus to the experimental group.
The control group should show a change in the dependent variable that is attributable only to the extraneous variation.
In contrast, the dependent variable in the experimental group should show a larger change caused by extraneous variation plus the test stimulus.
By subtracting the extraneous change (change in the control group) from the total change in the experimental group, one can estimate the amount of change due to the causal stimulus.
The second and most straightforward approach to controlling assignment error is matching.
It is a procedure for the assignment of subjects to groups; it ensures that each group of respondents is matched based on pertinent characteristics.
Suppose an experiment is to be conducted to examine if the mother’s education affects nutritional knowledge. It is apprehended that age is a factor that might influence knowledge.
To control by matching, we need to be sure that the age distribution of the mothers is the same in all groups.
Although matching assures that the subjects in each group are similar to the matched characteristics, the researcher can never be sure that the subjects have been matched on all characteristics that could be important to the experiment.
The disadvantage of matching is that any subject who does not have a matching partner on all relevant characteristics cannot be assigned to either group and thus cannot be used in the experiment.
Self-selection is another thorny problem in selecting a control group.
People who choose to enter a program are likely to be different from those who do not, and the prior differences (in interest, aspiration, values, initiative, etc.) make post-program comparisons between ‘served’ and ‘unserved’ groups risky.
Self-selection problems can sometimes be overcome if the subjects of both experimental and control groups are selected from volunteers.
Such selection can be thought of as a true experiment if the volunteers are randomly assigned to either group.
We emphasize here that randomization is the basic method by which equivalence between experimental and control groups is ensured. Experimental and control groups must be established so that they are equal.
It is best to assign subjects to experimental or control groups randomly. If the assignments are made randomly, each group should receive its fair share of different factors.
Matching and control are useful but do not account for all unknowns. They are supplemental ways of improving the measurement quality and reducing the extraneous noise in the measurement.
Advantages and Disadvantages of Experimental Study
Experimental research is seen as true research by many scientists. Yet there are many advantages and disadvantages of experimental research.
The advantages and disadvantages of any research are usually subjective, as one cannot claim that advantage in one experiment will also be an advantage in another.
Some people feel that human input is a disadvantage in these studies as humans always have their thoughts and can manipulate the results.
There is another thought that testing on humans is also a disadvantage as you cannot tell whether their answers or reactions are true or a show for the experiment.
We summarize below a few important advantages and disadvantages of an experimental study.
4 Advantages of Experimental Study
- In experimental studies, the researcher has control and the ability to change the experiment if the answers are inconclusive. This allows for less time-wasting in experiments;
- Contamination from extraneous variables can be controlled more effectively in experimental studies than in other designs. This helps the researcher to isolate experimental variables and evaluate their impact over time;
- The cost and convenience of experimentation are much less compared to other methods;
- The experiment provides the opportunity to study changes over time through repeated measurements. This replication leads to the discovery of an average effect of the independent variable across people, situations, and times;
8 Disadvantages of Experimental Study
- Most social sciences research is conducted in an artificial environment. This is perhaps the main problem with using experimentation in social sciences, where sufficient control is impossible in natural settings.
- It is sometimes impossible to control all the extraneous variables.
- With a large group of subjects, it is difficult to control the environment.
- Generalization from a non-probability sample can pose problems despite random assignment.
- Experimentation is most effectively targeted at problems of the present or immediate future. Experimental studies of the past are not feasible, and predictions are not possible in experimental studies.
- Intervention and control are the two important elements in experiments that are sometimes hard to achieve when ethical issues are involved.
- Scientist manipulates values, as a result of which they may not be making a completely objective experiment.
- People can be influenced by what they see and may give answers they think the researcher wants to hear rather than how they think and feel on a subject.
Types of Experimental Research Design

Pre-experimental Designs
Pre-experimental designs are those designs that do not have any comparison groups. Even if they have, they fail to meet the requirement of random assignment of these groups.
We will discuss a few pre-experimental designs;
- Posttest-only design;
- Pretest-Posttest design; and
- Static-group comparison.
Posttest-only design
The posttest-only design, also called the one-shot case study design, is the weakest of all designs and fails to control the various threats to internal validity adequately.
These designs are most useful for collecting descriptive information or doing small case studies of a particular situation.
It is diagramed as follows:
| Experimental Group: | X | O |
The design includes the following steps:
- Select the subjects
- Select the experimental environment
- Administer the experimental stimulus X
- Conduct the posttest with measurement O
As we can see, in this design, a program intervention (X) has been introduced, and sometimes after its introduction, a measurement observation (O) is made.
Since there is neither a control group nor a pretest measurement, there is no possibility of comparing the measurement O with any other measurement.
All that the measurement O can do is that it provides descriptive information.
By environment, we mean whether the experiment is conducted in the field or a laboratory setting or any other environment. The threats to the validity of history, maturation, selection, and experimental mortality cannot be controlled.
The lack of a pretest and a control group makes this design inadequate for establishing causality.
Example
UNICEF, Bangladesh, introduced a glucose injection campaign in certain IDD-prone areas of Bangladesh.
This is our intervention (X). A year later, a measurement was taken from those who received the injection resulting in the observation’ O.
Note that we have no means of controlling the extraneous influences. There should be some measure of what would happen when test units were not exposed to X compared to the measure when subjects were exposed to X.
Pretest-Posttest Design
This design includes a single experimental group, and it is called a pretest-posttest design with no control group.
Since this design lacks a control group with which to measure extraneous variation, it can be used only when the experimenter can assume that extraneous variation is minimal so that virtually all recorded changes in pre and posttest measurements are caused by the intervention (X), the test stimulus.
The design includes the following steps:
- Select the subjects
- Select the experimental environment
- Conduct the pretest with measurement O1
- Administer the experimental stimulus X
- Conduct the posttest with measurement O2
Example
The blood sample is taken to measure glucose level, and the glucose level is determined. This is our pretest observation, O1.
Two hours after administering glucose or breakfast, a second measurement was taken. This is our posttest measurement O2. The design is diagrammed as follows:
| Experimental Group: | O1 | X | O2 |
Since total variation in pre and posttest scores is being attributed to the causal factor, the formula for this cause is
| ΔExpt = O2 – O1 |
Suppose the experimenter’s assumption is incorrect and the extraneous factors cause a change in the pre and posttest scores.
In that case, the experimenter does not know how much of the change in the dependent variable is due to the intervention (X) and how much to uncontrolled factors.
We can address this problem by repeating the experiment and adding a control group with the pre and posttest but without intervention.
This design is subject to several threats to validity-history, testing, maturation, and instrumentation.
Static-Group Comparison
In the static group design, subjects are identified as either experimental or control groups.
The experimental group is measured after it has been exposed to the experimental treatment. Look at the following diagram that portrays the design:

Unlike the other two designs, this design adds a control group. The experimental group receives a program intervention (X) followed by a measurement observation (O1).
This measurement observation is then compared against a second observation (O2) from a control group that did not receive the program intervention.
The results of the static group design are then computed as a difference between the two observations as follows:
| ΔExpt = O2 – O1 |
The broken line ( – – – – – ) is a non-random line, which indicates that no random process was followed to create the two groups.
The addition of a comparison group makes a substantial improvement over the two designs. Its chief weakness is that there is no way to be certain that the two groups are equivalent and that no random process has been followed in creating the two groups.
True Experimental Designs
The major deficiency of the pre-experimental designs is that they fail to provide comparison groups that are truly equivalent. The way to achieve equivalence is through matching and random assignment.
We describe two such designs that fall under this category. These are;
Pretest-posttest control group design
It is a design in which all subjects are randomly assigned (RA) from a single population to the experimental and control groups. The experimental and the control groups receive an initial measurement observation (O1 and O3 in the accompanying diagram).
The experimental group then receives the program intervention (X), but the control group does not receive this intervention.
Finally, the second set of measurement observations ( O2 and O4 ) are made for both groups.
This design assumes that the effect of all extraneous variables will be the same on both the experimental and the control groups. The design is portrayed as follows:
| RA | Experimental Group | O1 | X | O2 |
| RA | Control Group | O3 | O4 |
We enumerate the steps in conducting a pretest-posttest control group design as follows:
| Experimental Group | Control Group |
| 1. Select subjects | 1. Select subject |
| 2. Select an experimental environment | 2. Select an experimental environment |
| 3. Take the pretest measurement (00 | 3. Take the pretest measurement (O3) |
| 4. Administer intervention (X) | 4. Administer no intervention. |
| 5. Take the posttest measurement (02) | 5. Take the posttest measurement (04) |
To assess the causal effect of the experimental treatment, we proceed as follows:
| ΔExpt = (O2 – O1) – (O4 – O3) |
We would expect that, since the experimental group received a special program intervention, O2 would be greater than O4. Also, since both the experimental and control cases were randomly assigned, we would expect that O1 would be equal to O3 on key variables.
Under this assumption, AExpt will be positive, and the amount contributing to this difference will be the true causal effect of the test stimulus. The control difference will equal the experimental difference in the cases in which the causal effect of the test stimulus is zero.
Because of the random assignment of subjects in the groups, this design suffers very little from the problems of validity threats.
Maturation, testing, and regression effects are handled well because one would expect them to be felt equally in experimental and control groups.
Mortality, however, can be a problem if there are different dropout rates in the study groups. The random assignment process well tackles the selection problem.
Posttest- only control group design.
In this design, the pretest measurements of both groups are omitted. Pretests are well established in classical research designs but are not necessary when the randomization process is followed.
The design is diagrammed as follows:
| RA | Experimental Group | X | O1 |
| RA | Control Group | O2 |
The experimental effect is measured by the difference between O1 and O2:
| ΔExpt = O1 – O2 |
The simplicity of this design makes it more attractive than the pretestposttest control group design.
Internal validity threats from history, maturation, selection, and statistical regression are adequately controlled by the random assignment.
Since the subjects are measured only once, the threats of testing and instrumentations are reduced, but differential mortality rates between experimental and control groups continue to be a potential problem.
Solmon four-group design
The Solmon four-group design is a way of avoiding some of the difficulties encountered in the pretest-posttest design.
This design contains two extra control groups, which reduce the influence of confounding variables and allow the researcher to test whether the pretest affects the subjects.
While much more complex to set up and analyze, the design type combats many internal validity issues plaguing research. It allows the researcher to exert complete control over the variables and allows the researcher to check that the pretest did not influence the results.
As we will observe from the diagram below, the Solmon four-group test is a standard pretest-posttest design, and the posttest only controls group design.
The various combinations of tested and untested groups with treatment and control groups allow the researcher to ensure that confounding variables and extraneous factors have not influenced the results.
| (A) | RA | Experimental group | O1 | X | O2 |
| (B) | RA | Control group | O3 | O4 | |
| (C) | RA | Experimental group | X | O5 | |
| (D) | RA | Control group | O6 |
The first two groups of the Solomon four-group design are designed and interpreted in the same way as in the pretest-posttest design and provide the same checks upon randomization.
Comparing the posttest results of groups C and D allows the researcher to determine if the actual act of pretesting influenced the results.
If the difference between the posttest results of Groups C and D is different from the Groups A and B difference, then the researcher can assume that the pretest has had some effect on the results.
Comparing the Group B Pretest and the Group D posttest allows the researcher to establish if any external factors have caused a temporal distortion.
For example, it shows if anything else could have caused the results shown and is a check upon causality.
The Comparison between Group A posttest and the Group C posttest allows the researcher to determine the effect that the pretest has had upon the treatment. If the posttest results for these two groups differ, then the pretest has had some effect on the treatment, and the experiment is flawed.
The comparison between the Group B posttest and the Group D posttest shows whether the pretest itself has affected behavior, independently of the treatment.
If the results are significantly different, then the act of pretesting has influenced the overall results and needs refinement.
Quasi-Experimental Designs
Quasi-experimental designs are those that do not satisfy the strict requirements of the experiment.
In such designs, subjects to be observed are not randomly assigned to different groups to measure the outcomes, as in a randomized experiment, but grouped according to a characteristic that they already possess.
Some authors distinguish between a natural experiment and a quasi-experiment. The difference is that the researcher manipulates the causal factor in a quasi-experiment, while in a natural experiment, the causal factor varies naturally.
The major disadvantage of quasi-experiments is that they are more open to confounding variables.
We have already pointed out that the best designs control relevant outside effects and lead to valid inferences about the program’s effects.
Unlike an experimental design, which protects against just about all possible threats to internal validity, quasi-experimental designs generally leave one or several of them uncontrolled.
In reality, it is simply impossible to meet the random assignment criteria of true experimental design.
Alongside this, researchers want to avoid the problems of validity threats associated with the pre-experimental designs.
The use of quasi-experimental designs in these circumstances offers a reasonable compromise, which does not have the restriction of random assignment.
It is, in this sense, inferior to a true experimental design but is usually superior to pre-experimental designs. We discuss a few quasi-experimental designs in this section. These are
- Non-equivalent control group design
- Time-series design
- Separate sample pretest-posttest design
- Ex-post facto design
Non-equivalent control group design
This is strong and probably the widely used quasi-experimental design. There is no random assignment to program and control as there would be in a true experiment.
There are two variants of this design. One is the so-called intact equivalent design, and the other is the self-selected experimental design.
In intact equivalent design, the membership in both groups is naturally assembled.
For example, we may use different classes in a school, hospital wards, or customers from similar stores. A major issue is making the comparison group as similar to the experimental group as possible.
Matching procedures are sometimes resorted to pairing up members of the experimental and control groups on available measures at the start of the program.
Afterward, when one group has been exposed to the benefits of the program and the other group has not, the difference between them should be attributed to the program intervention.
But matching for obvious reasons is much less satisfactory than randomized assignment on several counts. Not the least that we often cannot define the characteristics on which people should be matched.
That is, we do not know which characteristics will affect whether the person benefits from the program or not.
The second variant, the self-selected experimental design, is weaker because it encounters a problem in selecting a comparison group.
People who choose to enter a program are likely to differ from those who do not.
The prior differences (in interest, attitude, desire, norms, values, initiative, etc.) make post-program comparisons between ‘served’ and ‘un-served’ groups risky.
Self-selection problems can sometimes be overcome if the subjects of both experimental and control groups are selected from volunteers.
Such selection can be considered a true experiment if the volunteers are randomly assigned to either group. The design is diagrammed as follows:

A comparison of pretest results (O1– O3) indicates the degree of equivalence between the experimental and the control groups. If the pretest results are significantly different, there is a real question about the groups’ comparability.
On the other hand, if the pretest observations are similar between groups, there is more reason to believe that the experiment’s internal validity is good.
The non-equivalent control group design is particularly useful in evaluating training programs.
The design, however, is threatened by the selection effect and the interaction of selection with other factors. The regression effect would be an additional problem if groups were selected for extreme scores.
Time-series design
The time-series design is one of the most attractive quasi-experiments. It involves a series of measurements at periodic intervals before the program begins and continuing measurements after the program ends.
It thus becomes possible to determine whether the measures immediately before and after the program are a continuation of earlier patterns or whether they mark a decisive change.
A time-series design is similar to a pre-experimental design except that it has the advantage of repeated measurement observations before and after the program intervention (X).
Examine the following diagram:
| Experimental Group: | O1 | O2 | O3 | X | O4 | O5 | O6 |
Suppose we find no difference between O1, O2, and O3, but then a sudden increase occurs between O3 and O4, which subsequently continues to O5.
We can conclude with some degree of confidence that the sudden increase was probably due to the effect of the program intervention (X).
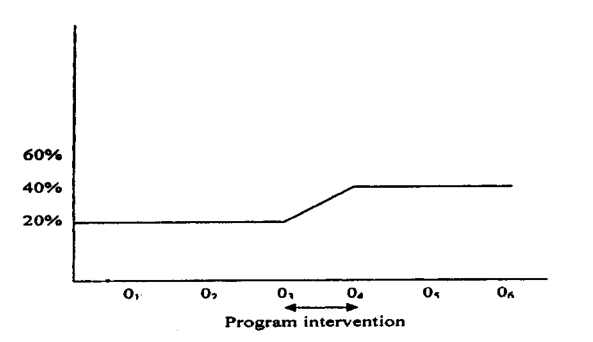
Figure: A time-series design showing the effect of the intervention
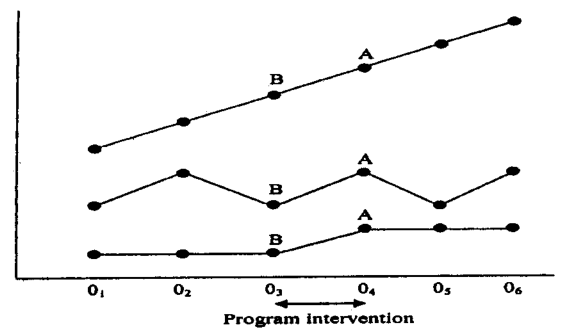
Figure: Three-time series displaying the varying significance
The figure is designed to illustrate the impact of intervention more vividly. The three cases shown in these figures will have different significance. Neither the top nor the middle tells us anything about the effect of the intervention.
The figure in the top displays a monotonous or continuous increase since the beginning of the study. In other words, the intervention does not impact the program.
The same interpretation is true for the figure in the middle. Only the change from B to A in the bottom figure can be attributed to the program effect. Note that this figure is similar.
The time-series design probably protects against almost all validity threats except history and instrumentation threats.
It allows for a more detailed analysis of data and program impact than the pretest-posttest design because it gives information on trends before and after program intervention. The time-series design helps the researcher avoid making a mistaken conclusion.
A time-series design is particularly appropriate when a researcher can make multiple measurement observations before and after a program intervention (Fisher et al. 1998: 87).
Once again, we note that the time series design recommended when using a control group is either impossible or not feasible for practical reasons.
Separate sample pretest-posttest design
This design is most applicable when we cannot know when and whom to introduce the treatment, but we can decide when and whom to measure.
Essentially, it involves doing a baseline pretest (O1) with a randomly selected sample from a study population.
Subsequently, a program intervention (X) is introduced, and then a posttest measurement (O2) is made using a second randomly selected sample from the same study population. The design is displayed as follows:
| RA: Pretest Group | O1 | (X) | |
| RA: Posttest Group | X | O2 |
The bracketed treatment (X) is irrelevant to the purpose of the study but is shown to suggest that the experimenter cannot control the treatment.
This is not a strong design because several threats to internal validity stand on the way. The history effect can confound the results by repeating the study at other times in other settings.
In contrast, it is considered superior to true experiments in external validity.
Its strength results from its being a field experiment in which the samples are usually drawn from the population to which we wish to generalize our findings.
Ex-post facto design
Sometimes it becomes difficult to divide the study population into two clear and similar groups.
This may be the case where the entire society consisting of different varieties of people and conditions are involved. It may be necessary to study the entire historical background of a country.
For instance, if a researcher is interested in studying the causes of the revolution, which is already in motion, he will not be able to objectively study the exact situation before the revolution started in the country.
He has to depend on the country’s historical background, which will be studied through the ex-post-facto study design.
In this particular instance, the investigator should select two countries: one in which revolution has taken place and the other in which it has not. The countries, otherwise, should broadly be similar.
Then, through a comparative study of the conditions of the two countries, the researcher may be able to find out the causes of the prevailing revolution.
In the ex-post-facto study, the past is studied through the present. But in other studies, we try to prognosticate the future from the present.
The most obvious limitation of the ex-post-facto study is the difficulty of finding two similar groups that are comparable. It is also difficult to find an objective criterion of comparison.
Secondly, it is impossible to create artificial conditions or have controlled conditions for study.
Thirdly, employing a pretest-posttest design in such a study is impossible.
Conclusion
The primary objective of experimental research design is to determine how well a particular program achieves its goals by controlling the contamination of the relationship between independent and dependent variables.
The main types of experimental research design are Pre-experimental Designs, True Experimental Designs, and Quasi-Experimental Designs.
How does an experimental study differ from a correlational study?
An experimental study involves the researcher manipulating the situation and measuring the outcome of this manipulation, aiming to establish causation. In contrast, a correlational study has limited control over the research environment and primarily identifies relationships without establishing causation.
What is the difference between the experimental group and the control group in an experimental study?
In an experimental study, the group that receives the test stimulus or manipulation is called the experimental group. The group that does not receive the test stimulus is referred to as the control group.
What are the three main characteristics of a classical experimental study?
The three main characteristics of a classical experimental study are Manipulation, Control, and Randomization.
What does “randomization” mean in the context of experimental research?
In experimental research, randomization refers to the process of randomly assigning subjects to the control and experimental groups, ensuring each subject has an equal chance of being placed in either group. This helps make the groups as similar as possible regarding the dependent variable.

