The law of equi-marginal utility is simply an extension of the law of diminishing marginal utility to two or more than two commodities. In cardinal utility analysis, this law is stated by Lipsey in the following words:
“The household maximizing the utility will so allocate the expenditure between commodities that the utility of the last penny spent on each item is equal.” As we know, every consumer has unlimited wants.
However, his income at any time is limited. The consumer has to choose among many commodities that he can and would like to buy. He, therefore, consciously or unconsciously compares the satisfaction which he obtains from the purchase of the commodity and the price which he pays for it.
If he thinks the utility of the commodity is greater or at least equal to the loss of utility of the money price, he buys that commodity.
As he buys more and more of that commodity, the utility of the successive units begins to diminish. He stops further purchase of the commodity at a point where the marginal utility of the commodity and its price are just equal.
If he pushes the purchase further from his point of equilibrium, then the marginal utility of the commodity will be less than that of the price, and the household will be a loser. A consumer will be in equilibrium with a single commodity symbolically: MUX = PX.
A prudent consumer, to get the maximum satisfaction from his limited means, compares not only the utility of a particular commodity and the price but also the utility of the other commodities which he can buy with his scarce resources.
If he finds that a particular expenditure is yielding less marginal utility, he will try to transfer a unit of expenditure to another commodity for higher marginal utility.
The consumer will reach his equilibrium position when it will not be possible for him to increase the total utility by using other goods. The position of equilibrium will be reached when the marginal utility is equal to its price, and the ratio of the prices of all goods is equal to the ratio of their marginal utilities.
The consumer will maximize total utility from his income when the utility from the last unit spent on each good is the same.
Algebraically, this is MUa / Pa = MUb / Pb = MUc / Pc – MUn / Pn. Here: a, b, c… n are various goods consumed.
Assumptions of the Law of Equi-Marginal Utility
The main assumptions of the law of equi-marginal utility are as follows:
Independent Utilities
The marginal utilities of different commodities are independent of each other and diminish with more and more purchases.
Constant marginal utility of money
The marginal utility of money remains constant to the consumer as he spends more and more of it on the purchase of goods.
Utility is cardinally measurable
It is assumed that utility is a quantifiable entity. This means that a person can express the satisfaction derived from the consumption of a commodity in quantitative terms.
Every consumer is rational in the purchase of goods
Here we may take it that a person would show normal behavior in the purchase of goods.
Example and Explanation of Law of Equi-Marginal Utility
The doctrine of equi-marginal utility can be explained by taking an example. Suppose a person has Tk.5 with him, which he wishes to spend on two commodities, tea and cigarettes. The marginal utility derived from both these commodities is as follows:
| Units of Money | MU of Tea | MU of Cigarettes |
| 1 | 10 | 12 |
| 2 | 8 | 10 |
| 3 | 6 | 8 |
| 4 | 4 | 6 |
| 5 | 2 | 3 |
| Tk.5 | Total Utility = 30 | Total Utility = 39 |
A rational consumer would like to get maximum satisfaction from $5.00. He can spend money in three ways:
- 1. Tk.5 may be spent on tea only.
- 2. Tk.5 may be utilized for the purchase of cigarettes only.
- 3. Some Taka may be spent on the purchase of tea and some on the purchase of cigarettes.
If the prudent consumer spends Tk.5 on the purchase of tea, he gets 30 utility. If he spends Tk.5 on the purchase of cigarettes, the total utility derived is 39 which is higher than tea. To make the best of the limited resources, he adjusts his expenditure.
- 1. By spending Tk.4 on tea and Tk.l on cigarettes, he gets 40 utility (10+8+6+4+12 = 40).
- 2. By spending Tk.3 on tea and Tk.2 on cigarettes, he derives 46 utility (10+8+6+12+10 = 46).
- 3. By spending Tk.2 on tea and Tk.3 on cigarettes, he gets 48 utility 10+8+12+10+8 = 48).
- 4. By spending $1 on tea and Tk.4 on cigarettes, he gets 46 utility (10+12+10+8+6 = 46).
The prudent consumer will spend I k.2 on tea and I k.3 on cigarettes and will get maximum satisfaction. When he spends Tk.2 on tea and Tk.3 on cigarettes, the marginal utilities derived from both these commodities is equal to 8.
When the marginal utilities of the two commodities are equalized, the total utility is then maximum, i.e., 48 as is clear from the schedule given above.
Curve/Diagram of Law of Equi-Marginal Utility
The law of equi-marginal utility can be explained with the help of diagrams.
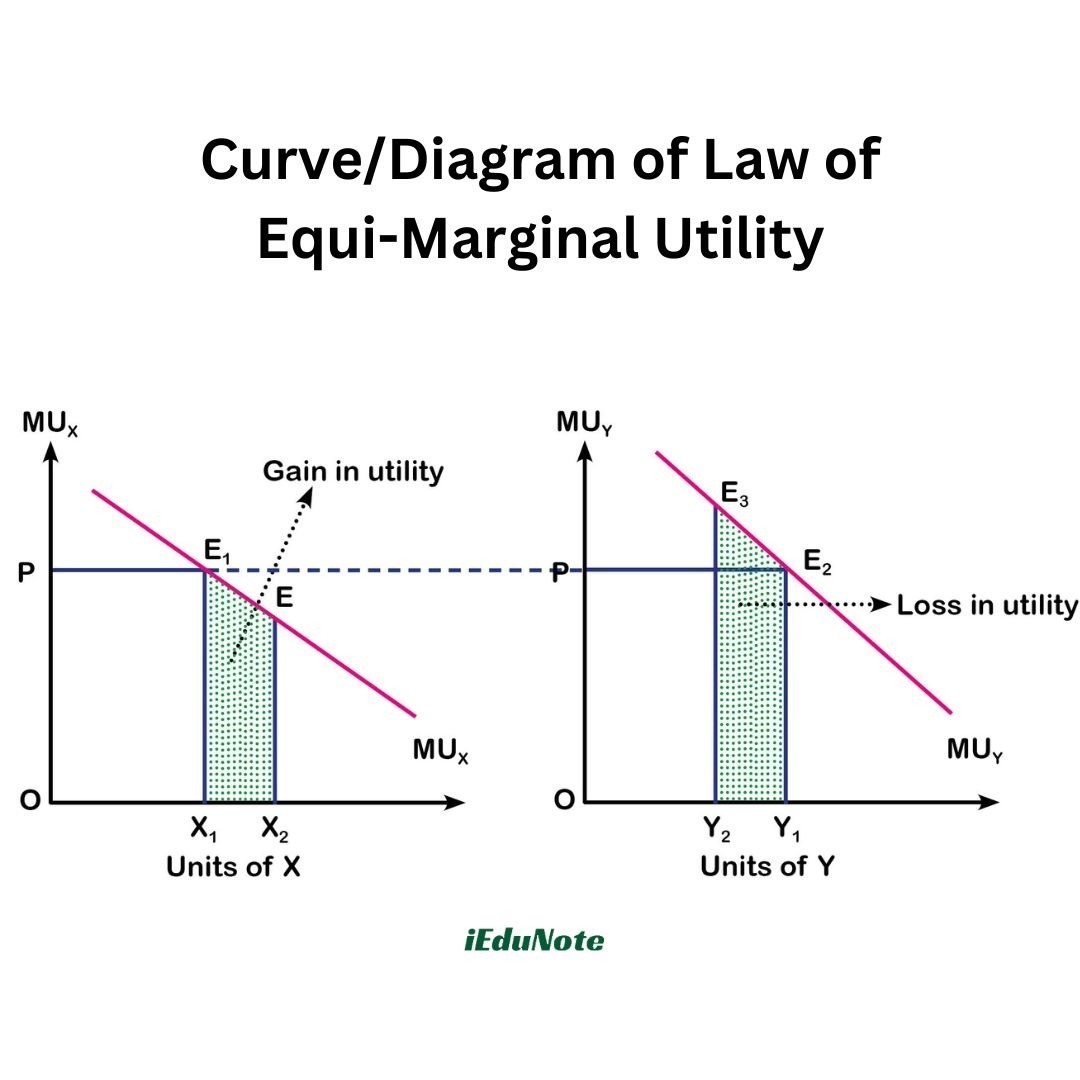
In Figure 2.3, MU is the marginal utility curve for tea and KL for cigarettes. When a consumer spends OP amount (Tk.2) on tea and OC (Tk.3) on cigarettes, the marginal utility derived from the consumption
of both the items (Tea and Cigarettes) is equal to 8 units (EP = NC).
The consumer gets the maximum utility when he spends Tk.2 on tea and Tk.3 on cigarettes and by no other alternative in the expenditure.
We now assume that the consumer spends Tk.l on tea (OCZ amount) and Tk.4 (OOZ) on cigarettes. If COZ more amounts are spent on cigarettes, the added utility is equal to the area COZNZN. On the other hand, the
expenditure on tea falls from OP amount (Tk.2) to OCZ amount (Tk.l). There is a loss of utility equal to the area CZPEEZ. The loss in utility (tea) is greater than that of the gain in utility (cigarettes).
Therefore, there should be a loss in maximum satisfaction except the combination of expenditure of Tk.2 on tea and Tk.3 on cigarettes.
This law is known as the Law of maximum Satisfaction because a consumer tries to get maximum satisfaction from his limited resources by planning his expenditure so that the marginal utility of a Dollar spent in one use is the same as the marginal utility of a Dollar spent on another use.
It is known as the Law of Substitution because the consumer continuously substitutes one good for another till he gets the maximum satisfaction.
It is called the Law of Indifference because the maximum satisfaction has been achieved by equating the marginal utility in all the uses. The consumer then becomes indifferent to readjusting his expenditure unless some change takes place in his income or the prices of the commodities, etc.
Limitations/Exceptions of Law of Equi-Marginal Utility
Effect on fashions and customs
The law of equi-marginal utility may become inoperative if people are forced by fashions and customs to spend money on the purchase of those commodities which they know less utility but cannot transfer the unit of money from the less advantageous uses to the more advantageous uses.
Ignorance or carelessness
Sometimes people due to their ignorance of price or carelessness to weigh the utility of the purchased commodity do not obtain the maximum advantage by equating the marginal utility in all the uses.
Indivisible units
If the unit of expenditure is not divisible, then again the law may become inoperative.
Freedom of choice
If there is no perfect freedom between various alternatives, the operation of law may be impeded.
Importance of Law of Equi-Marginal Utility
The law of equi-marginal utility is of great practical importance. The application of the principles of substitution extends over almost every field of economic inquiry.
Every consumer consciously trying to get maximum satisfaction from his limited resources acts upon this principle of substitution. The same is the case with the producer.
In the field of exchange and in the theory of distribution too, this law plays a vital role. In short, despite its limitation, the law of maximum satisfaction is a meaningful general statement of how consumers behave.
In addition to its application to consumption, it applies equally to the theory of production and the theory of distribution.
In the theory of production, it is applied to the substitution of various factors of production to the point where the marginal return from all the factors is equal. The government can also use this analysis for the evaluation of its different economic prices.
The equal marginal rule also guides an individual in the spending of his savings on different types of assets. The law of equi marginal utility also guides an individual in the allocation of his time between work and leisure.
In short, despite limitations the law of substitution is applied to all problems of allocation of scarce resources.
Derivation of the Demand Curve in terms of Utility Analysis:
Professor Alfred Marshal was of the view that the law of demand and the demand curve can be derived with the help of utility analysis.
He explained the derivation of the law of demand:
- 1. In the case of a single commodity and
- 2. in the case of two or more than two commodities.
In the utility analysis of demand, the following assumptions are made:
Assumptions
- 1. Utility is cardinally measurable.
- 2. Utilities of different commodities are independent.
- 3. The marginal utility of money to the consumer remains constant.
- 4. Utility gained from the successive units of a commodity diminishes.
Derivation of Demand Curve in the Case of a Single Commodity (Law of Diminishing Marginal Utility)
Professor Alfred Marshall derived the demand curve with the help of the law of diminishing marginal utility. The law of diminishing marginal utility states that as the consumer purchases more and more units of a commodity, he gets less and less utility from the successive units of the expenditure.
At the same time, as the consumer purchases more and more units of one commodity, then a lesser and lesser amount of money is left with him to buy other goods and services.
A rational consumer, before, while purchasing a commodity compares the price of the commodity which he has to pay with the utility of a commodity he receives from it.
So long as the marginal utility of a commodity is higher than its price (MUX > Px), the consumer would demand more and more units of it till its marginal utility is equal to its price MUX = Px or the equilibrium condition is established.
To put it differently, as the consumer consumes more and more units of a commodity, its marginal utility diminishes.
So it is only at a diminishing price at which the consumer would like to demand more and more units of a commodity.
Diagram/Curve:
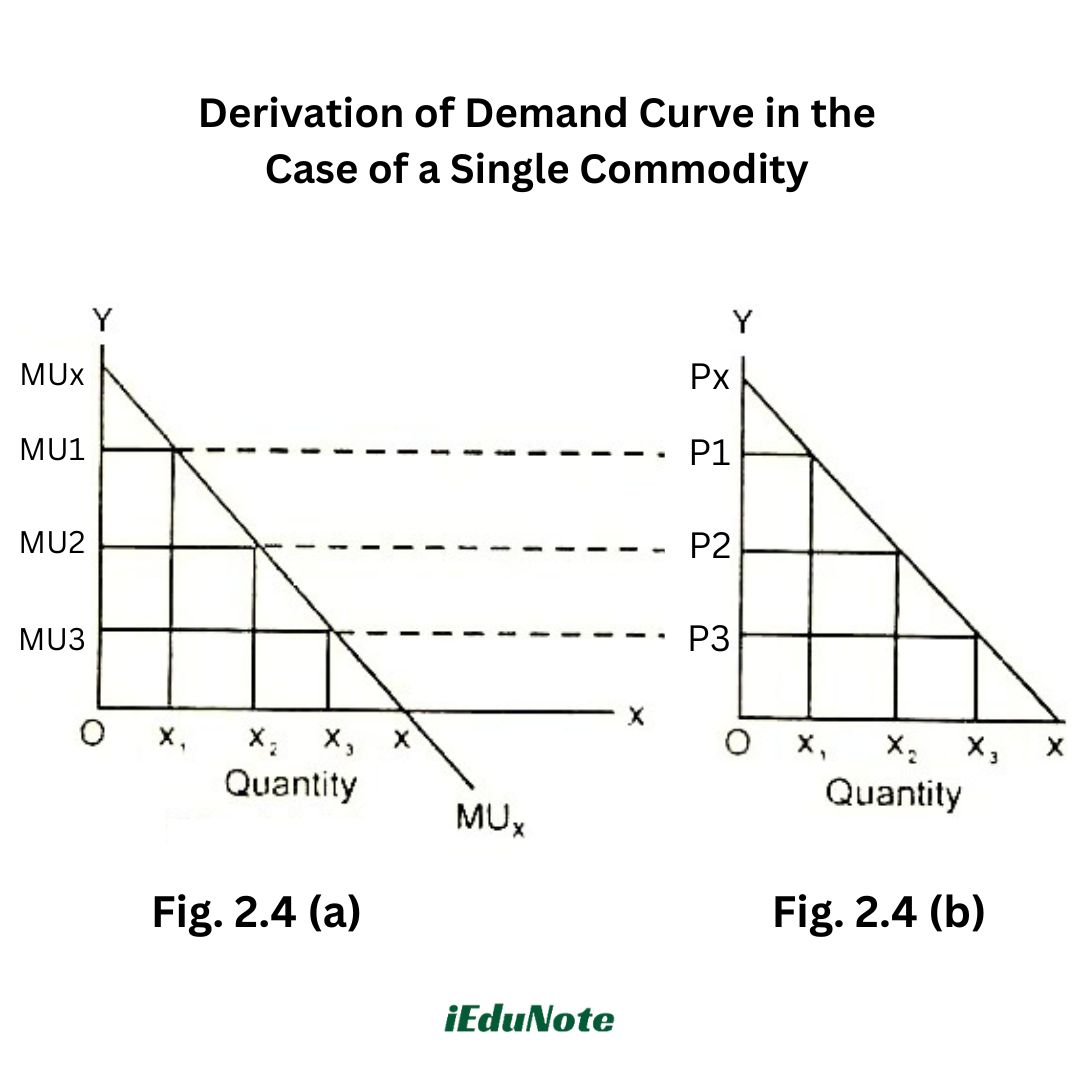
In Fig. 2.4(a), the MU curve is negatively sloped. It shows that as the consumer acquires larger quantities of good X, its marginal utility diminishes. Consequently, at diminishing prices, the quantity demanded of good X increases, as is shown in Fig. 2.4(b).
At X1, the quantity, the marginal utility of a good is MUX1. This is equal to P1 by definition. The consumer here demands OX1 quantity of the commodity at price P1. In the same way, the X2 quantity of the good is equal to P2.
Here, at price P2, the consumer will buy an OX2 quantity of the commodity. At X3 quantity, the marginal utility is MUX3, which is equal to P3. At price P3, the consumer will buy OX3 quantity, and so on.
We conclude from the above that as the purchase of the units of commodity X is increased, its marginal utility diminishes. So, at diminishing prices, the quantity demanded of good X increases, as is evident from Fig. 2.4(b).
The rational consumer supports the notion of a downward-sloping demand curve, meaning that when the price falls, other things remain the same, and the quantity demanded of a good increases, and vice versa. (The negative section of the MU curve does not form part of the demand curve, since negative quantities do not make sense in economics).
Derivation of the Demand Curve in the Case of Two or More than Two Commodities (Law of Equi-Marginal Utility)
The law of equi-marginal utility can be applied in the case of two or more two goods. When a consumer has to spend a certain given income on several goods, he attains maximum satisfaction when the marginal utilities of the goods are proportional to their prices, as stated below:
MUX / PX = MUY / PY = MUN / PN
Derivation of Demand Curve:
In Fig. 2.5(a), (b), and (c), given the money income, the price of commodity X (PX), the price of commodity Y (PY), and the constant marginal utility of money (MUM), the demand curve derived is illustrated.
The consumer allocates his money income between X and Y commodities to get OQi units of good X and OY units of good Y commodities because the combination corresponds to:
MUX / PX = MUY / PY = MUM
At the OM level (constant).
Diagram/Curve:

Let us assume that money income and price of Y commodity remain constant but the price of X commodity decreases. As a result of this money expenditure on commodity X rises resulting MUr / Px curve shifting towards the right.
The consumer now allocates his income to OQ2 quantity of X commodity and OY quantity of Y commodity because the combinations correspondence to/ Px = MUy / Py = MUm(constant) at OM level.
Thus in response to a decrease in the price from Px to Pxj, the quantity demanded of a good X increases from OQi to OQ2. The DD is a negatively sloped demand curve.
Consumer’s surplus:
The surplus utility over the price a consumer gets by buying a good is termed as consumer’s surplus. Consumer surplus is the difference between the prices a consumer is willing to pay and the price he pays. According to Professor Taussig, “consumer’s surplus is the difference between the potential price and the actual price”
Therefore, the consumer’s surplus is derived from the law of diminishing marginal utility. According to this law, the consumer is ready to pay different prices for different units of goods.
Because with the increasing consumption the marginal utility of that good decreases continuously. In this situation the marginal utility and price of a good becomes equal. At a particular time, all units of a good are bought and sold at a unique price.
Suppose the consumer is ready to pay $50 for 1st orange, Tk.40 for 2nd orange, Tk.30 for 3rd orange and $20 for 4th orange. In the market, each orange is sold for Tk, 20. Therefore, for four oranges total expenditure is 4×20 = 80. But by purchasing 4 oranges the consumer will get the utility equivalent of $(50+40+30+20) =140. In this case, the consumer will get surplus utility (140-80) =60 equivalent to Tk.60.
It is the consumer’s surplus. The consumer’s surplus is shown in the following table:
| Unit of good | Market price (Taka) | Utility earned from each unit (Taka) | Consumer’s surplus (Taka) |
|---|---|---|---|
| 1st orange | 20 | 50.0 | 30.0 |
| 2nd orange | 20 | 40.0 | 20.0 |
| 3rd orange | 20 | 30.0 | 10.0 |
| 4th orange | 20 | 20.0 | 0.0 |
| Total oranges | $80.0 | $140.0 | $60.0 |
Consumer surplus can be shown in the following graph. The graph shows that the OX axis indicates the quantity of goods and OY axis indicates price and marginal utility, and DD is the demand of the marginal utility curve of the good.
OP is the market price of the good. If the consumer purchases the OQ amount at the OP price then the OP price equals the marginal utility MQ and the consumer attains the equilibrium condition. The consumer’s earns the OQ quantity and earns the utility of OQMD. But he expends OQMP.
Here, the consumer’s surplus is = OQMD – OQMP PMD. This PMD is the consumer’s surplus.
Therefore, a consumer’s surplus is the difference between the prices a consumer is willing to pay and the price he pays.

