The formula we have considered in sample size calculation applies to designs based on the equal probability selection method (such as SRS, proportionate stratified sample).
Still, very few practical designs are as straightforward as this. As a result, the preceding formulae no longer apply but are replaced by others.
We recognize that complex designs provide less precise estimators than an Epsom design of the same size.
This loss arising out of using complex designs can sometimes be circumvented by using what is known as the design effect (deff).
The design effect is defined as the ratio of the actual variance of the sample estimate obtained from a particular design to the variance of a simple random sample estimate of the same size.
The “deff” for a stratified sample is typically less than one, implying variance reduction due to stratification. In cluster samples, the “deff” is typically larger than one expressing the loss due to clustering.
A “deff” larger than one would imply an upward adjustment needed in the sample size calculated with a simple random sample.
The sample size required for a cluster survey is almost always larger than that required for a random or stratified sample because of the “deff” factor.
If the prevalence of a condition is approximately the same in each cluster, the “deff” will be around the null value ‘one.’ The greater the clusters differ in terms of the estimates of the parameters, the larger the “deff.”
As the “deff” increases, the sample size must increase to maintain a desired level of precision. The formula used for calculating sample size for estimating n in a large population is thus a modification of the formula (c):
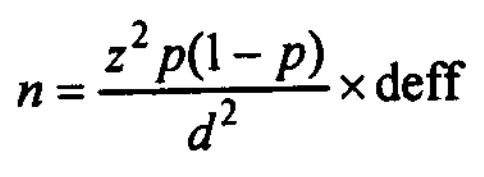
A design effect, thus, is seen to serve two purposes;
- estimation of sample size, and
- appraising the efficiency of more complex designs.
Example of Design Effect
In a simple random sample of 50 households of 120 persons, 27% were found to possess a mobile set. The sampling variances under a complex sampling design and simple random sampling of persons were computed to be 0.015 and 0.006, respectively.
Compute the design effect and estimate the sample size needed to achieve an equivalent level of precision as is possessed by the simple random sample of 50 households.
Solution: The estimated design effect (deff) is;
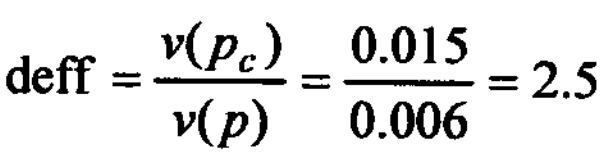
Hence the sample size must be raised to; n = 50 x 2.5 = 125.
A sample of 125 households is expected to compensate for the loss of efficiency due to the use of the complex design.

